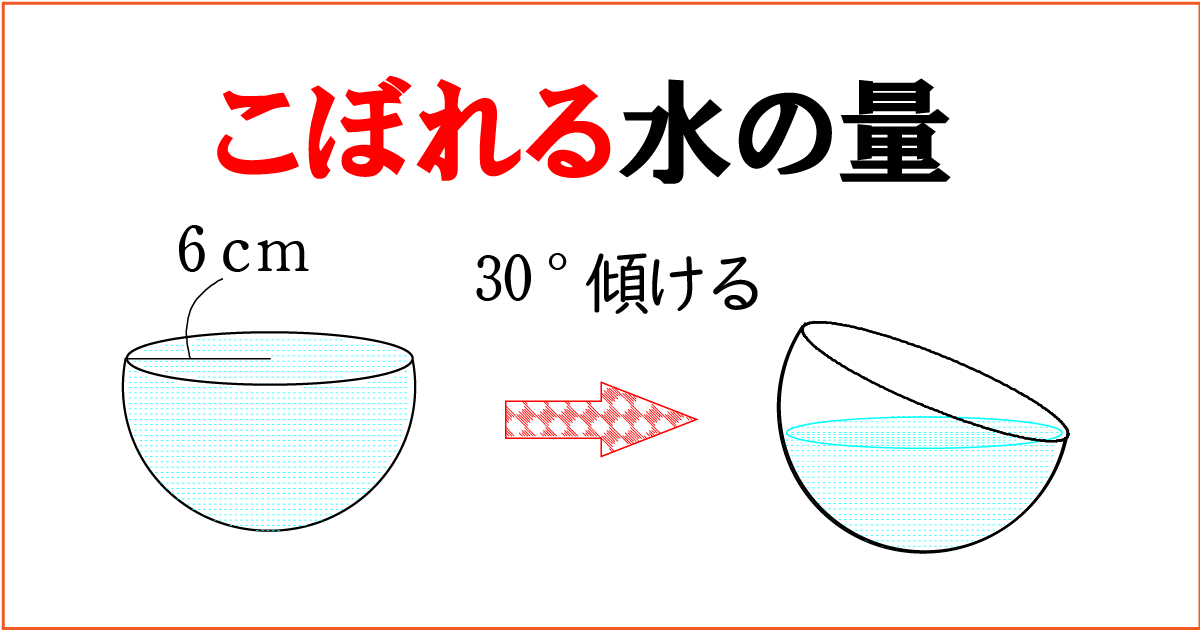
水が入った容器がある。
この容器は半径 \(6cm\) の半球を図のように使うものとします。
半径 \(r\) の球の体積は \(\frac{4}{3}\pi r^3\) ということで,
一見カンタンそうに見える本題。
その直感は正しいのでしょうか?
図をかく
基本ですね。
図をかいて,結論を求めるために考えるべきことを見出しましょう。
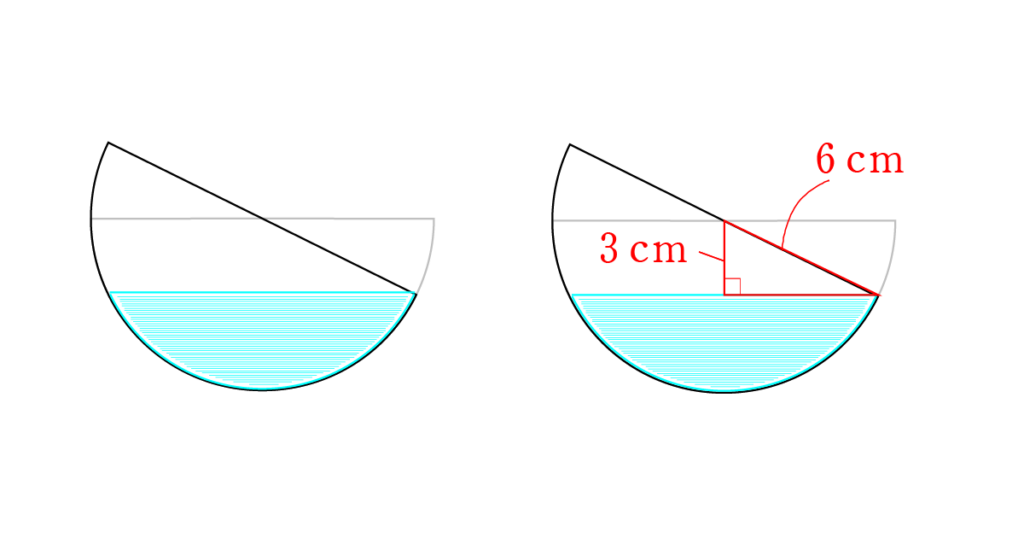
図のように,容器の立面図をかきます。(傾けた後の容器は濃い線)
ここからわかること,傾ける角度が \(30^{\circ} \) だから,
水面は半球の底面の中心から \(3 cm\) の深さにあるということ!
これをもとに座標平面に表すと・・・
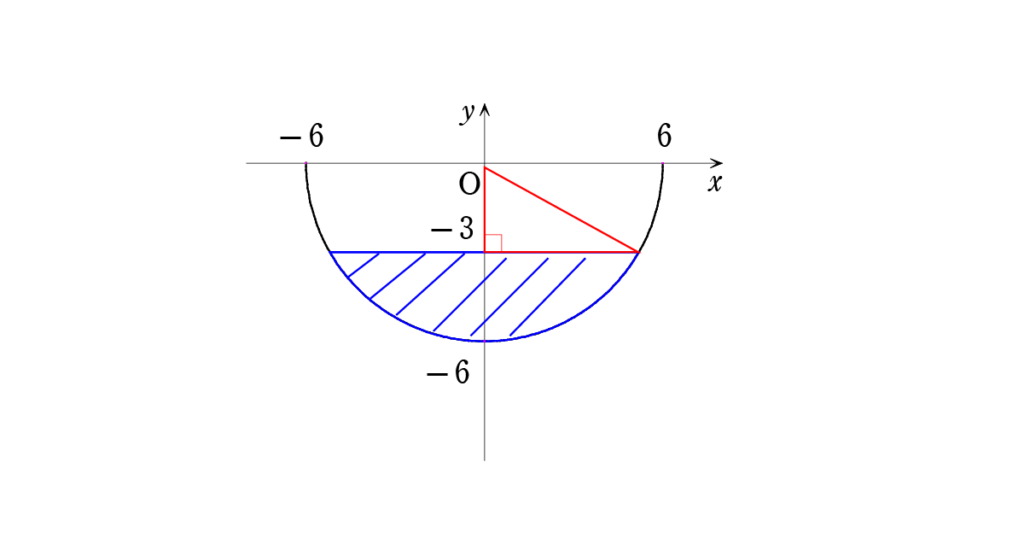
残った水の量,つまり体積は
「青色の部分を \(y\) 軸を回転の軸として1回転させた立体」の体積なのです。
曲線 (弧) の式は \(y=\sqrt{6^2-x^2}\) ( \(-6 \text{≦} x \text{≦} 6\) )
回転体の体積 \(V=\pi \int_{-6}^{-3} y^2 dx \)
続けます。
\(V=\pi \int_{-6}^{-3} y^2 dx \)
\(=\pi \int_{-6}^{-3} (36-x^2) dx \)
\(=45 \pi \) ( \(cm^3\) )
こぼれた水の量は 半球の 容積から \(V\) をひくことで求めます。
すなわち
\(\frac{1}{2}\times \frac{4}{3} \pi \times{6^3}-V\)
\(=99 \pi (cm^2) \) (結論)
公式もあるよ!
半球の半径 \(r\) ,傾ける角度を \(\theta\) とすると,
(こぼれる水の体積) \(=\frac{\pi}{3}r^3 \sin{\theta}(3-\sin^2{\theta})\)
(残る水の体積) \(=\frac{\pi}{3}r^3(\sin^2{\theta}-3\sin{\theta}+2)\)
となり,すべての水がこぼれる (残る水の体積が \(0\) ) のは
\(\sin^2{\theta}-3\sin{\theta}+2=0\) ,
すなわち \(\theta=90^{\circ}\) のときだとわかります。( \(0^{\circ} \text{≦} \theta \text{≦} 90^{\circ}\) )
あとがき ① : まずは図をかく!
本題のように,直観では捉えにくい課題に出会うことがあります。
今回は,
満水の器 → 器を傾ける → 器を戻す → 立面図をグラフにする
というフローで図示しました。
これにより 残った水の深さが明らかになったわけです。
このように,図示によって課題の本質が見えてくるもので,
「困ったら図示」「とりあえず図示」という習慣を持っていたいものですね。
あとがき ② : それでも直観は捨てられない
直観の弱さを補う ための図示のお話でした。
ただ,この図示が不完全ならどうでしょう。
たとえば,
明らかに鈍角三角形になる図形をかいた結果,「鋭角三角形にみえる」とか,
三角形の頂点が円の外側にある条件だが,「三角形が円に内接している」とか・・・
この場合,「条件」と「図示」の乖離が大きく,思考を困難にすることでしょう。
だからこそ,「図示はなるべく正確に」ということを大切にしたいのです。
大学入試や共通テストなどでは,1つの大問に次々と条件が与えられます。
はじめに,その大問の全体観をつかみ,
「円が登場するのか?」「平面 & 空間?」「垂直は登場する?」
などの正確な図示に不可欠の要素をさがしにいってください。




コメント