共通な因数は無いけれど…
因数分解の基本として,「共通な因数をくくり出す」というものがあります。
本題の式 \(a^2bd+ab^2c+bc^2d+acd^2\) には
共通な因数は無いのですが,
左2つの項 \(a^2bd\) , \(ab^2c\) には
共通な因数 \(ab\) があり,
右2つの項 \(bc^2d\) , \(acd^2\) には
共通な因数 \(bc\) があります。
これを試してみましょう!
すなわち…
\(a^2bd+ab^2c+bc^2d+acd^2\)
\(=ab(ad+bc)+cd(bc+ad)\) \(=(ab+cd)(ad+bc)\)
たすきがけ
因数分解といえばコレ。
最初にすべきことは,式を降べきの順に整理すること!
今回は \(a\) について整理します。
( \(a\) について次数の大きい項から順に並べる)
\(a^2bd+ab^2c+bc^2d+acd^2\)
\(=bda^2+(b^2c+cd^2)a+bc^2d\)
さらに整理して…
\(bda^2+c(b^2+d^2)a+bc\times{dc}\)
で,たすきがけ!
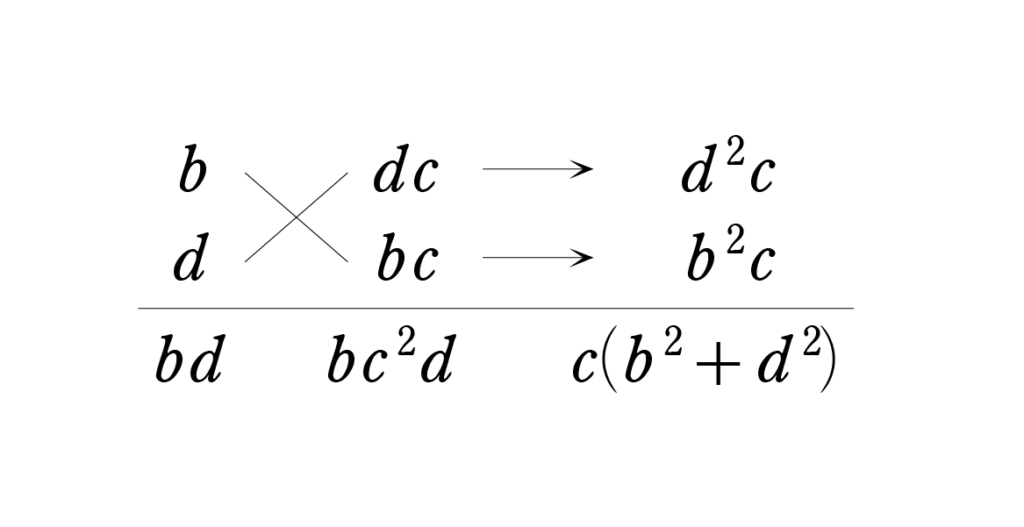
これにより
\(bda^2+c(b^2+d^2)a+bc\times{dc}\)
\(=(ab+cd)(ad+bc)\)
あとがき : 因数分解の “型” を的中させるセンス
本題は 「一部の項に共通な因数を見出す」「たすきがけ」といった方法で解決しました。
このように,因数分解のアプローチは1通りのみとは限りません。
一方で,「最適 (最も楽) 」が存在したり,「定番の アプローチ をすべて試したがうまくいかない」という 場合があったりと,因数分解の幅広さを実感することがあるでしょう。
上級者は この 最適のアプローチ を素早く見出します。
このセンスを磨くためには・・・
やはり,たくさんの 問題に出会い,たくさんの試行を積み上げることでしょうか?
因数分解の問題だけではない。
関数,微積・・・ すべてです!





コメント