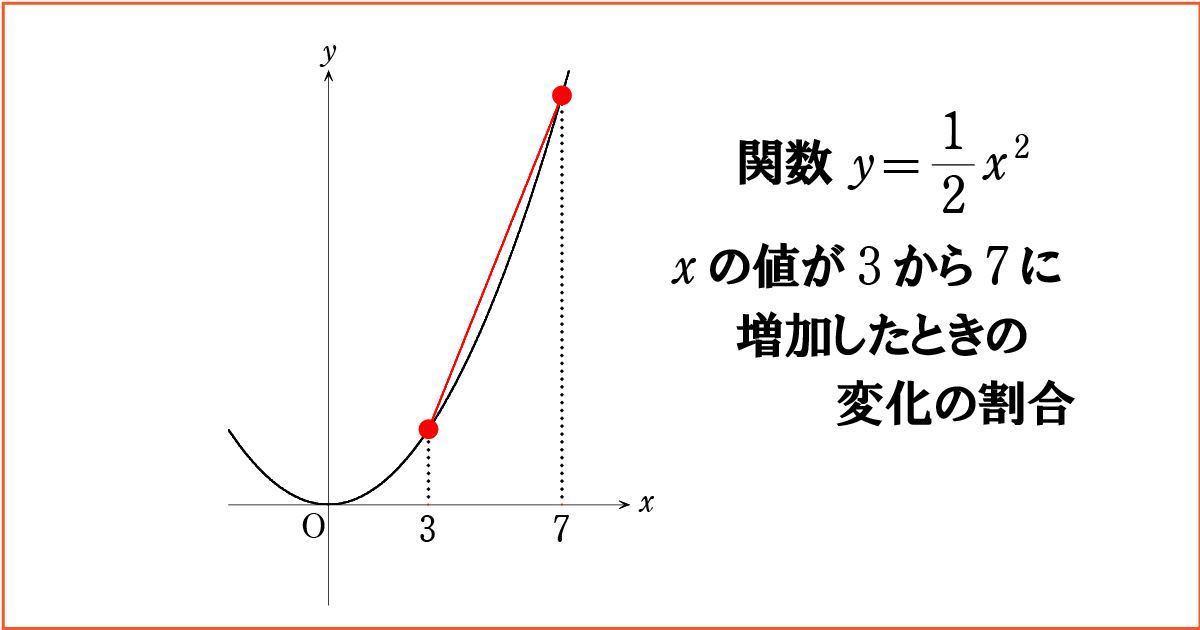
\(y=\frac{1}{2}x^2\)
\(x\) の値が \(3\) から \(7\) に増加したときの変化の割合!
中学校の教科書にもあるこの課題。
教科書と同じ解法はもちろん,教科書には無い裏ワザ的解法も紹介します。
解法 1 スタンダード
変化の割合は \(\frac{(y の増加量)}{(x の増加量)}\) によって求められます。
つまり,\(x\) の増加量 と,\(y\) の増加量 を知ることができればよいわけです。
〇 変化前 と 変化後 をまとめる
\(x\) は \(3\) → \(7\) という変化です。
では,\(y\) はどうでしょう。
変化前,変化後の \(y\) の値がわからないので求めておきます。
これはそれぞれ \(x\) が \(3\) のときの \(y\) の値,
\(x\) が \(7\) のときの \(y\) の値 だから,
変化前 \(y=\frac{1}{2}\times3^2=\frac{9}{2}\)
変化後 \(y=\frac{1}{2}\times7^2=\frac{49}{2}\)
\(x\) \(3\) → \(7\)
\(y\) \(\frac{9}{2}\) → \(\frac{49}{2}\)
〇 変化の割合 を求める
\(x\) の増加量は \(7-3=4\)
\(y\) の増加量は \(\frac{49}{2}-\frac{9}{2}=20\)
\((変化の割合)=\frac{20}{4}=5\)解法 2 裏ワザ的解法
これはホントにシンプルかつ簡単。
用意するのは
定数 \(\frac{1}{2}\)
変化後と変化前の \(x\) の値 \(3\) と \(7\)
これを
\((変化の割合)=\frac{1}{2}\times(3+7)=5\)こうして解決です。
まとめると
\((変化の割合)= (定数)\times(\quad x_{1} + \quad x_{2})\)あとがき : 高みをめざすなら 裏ワザ ではなく 常識
2つめの解法は「裏ワザ的」と表現しました。
学校で扱われることは (先生が自発的に) 珍しいようですね。
学校の先生の意見として,
「こんな裏ワザを教えると,基本がメチャクチャになる。」
というものが多くあります。(実際に聞いた)
まぁ,確かにその通りかも・・・
とはいえ,私が中学校教員のときには,例外なく伝えてきましたがね(笑)。
中学校以後の数学では,一般化 というものを大切に考えるべきで,
\(\frac{(y の増加量)}{(x の増加量)}\)を一般化しようとすると 約分作業を経験して・・・
様々な過程を学んで・・・
公式が誕生するわけです。
学校の先生には嫌われがちですが,より高い水準で数学に向き合う人にとってはマストの公式です。
数学では,解法は1つとは限らない。
「より深く網羅的な理解」 は 「複数の解法を扱うことができる」
の必要十分条件です!




コメント