円柱の表面積

定番の表面積問題。

　

教科書にある解法　と　公式による解法

　

を武器に 解決しましょう！

　

教科書の解法

面積をもつ ⇒ 平面に表すことができる

　

なので，これは円錐の展開図をかくことで平面に表してみます。

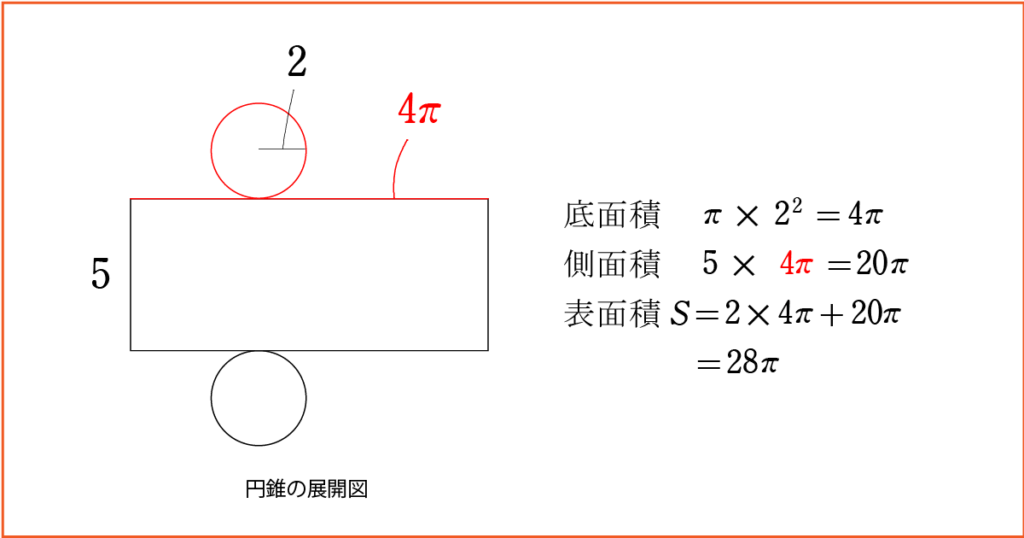
底面である円が \(2\) つ，

　

側面である長方形が \(1\) つ確認できます。

　

底面は半径が \(2\) の円だから

　

底面積は　\(\pi\times2^2=4\pi\)

　

側面は縦が \(5\) 横が \(4\pi\) (底面の円の円周に一致) だから

　

側面積は　\(5\times4\pi=20\pi\)

　

というわけで，表面積は

(底面積) \(\times\) \(2\) \(+\) (側面積)　であるから

　

表面積 \(S=4\pi\times2+20\pi=28\pi\)

　

公式による解法

(値) が決まるとそれに従って (新しい値) が１つに決まる。

　

そんなとき，(値) と (新しい値) との関係を等式で表すことができます。

　

例) 長方形の縦と横が決まれば面積が１つに決まる。

　

この等式は公式として確立されます。

　

そして，円柱の表面積を決定する値は

・底面の円の半径

・高さ

であり，これを用いて公式を導出することができます。

　

底面の半径　を \(r\)

高さ　を \(h\)

　

として展開図をかくと…　

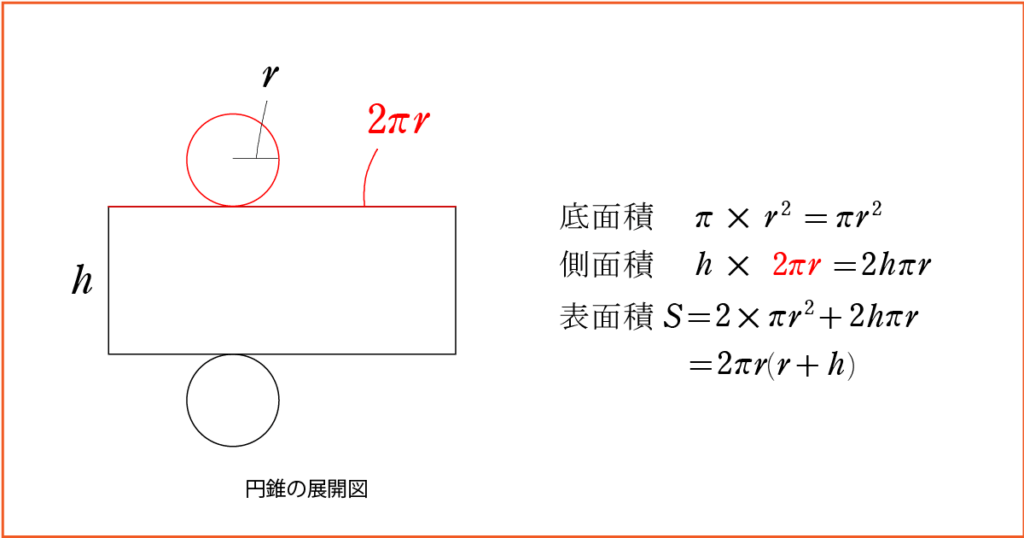
(底面積) \(\pi \times r^2=\pi r^2\)

　

側面の横の長さは \(2\pi r\) と表され，

　

(側面積) \(=h\times2\pi r=2h\pi r\)

　

よって表面積 \(S\) は

　

\(S=2\times\pi r^2+2h\pi r\)

　\(=2\pi r(r+h)\)

　

公式

底面の半径が \(r\) ，高さが \(h\) の円柱の表面積 \(S\) は

\(S=2\pi r(r+h)\)

　

本題では，

\(r=2\) ，\(h=5\) だから

\(S=2\pi\times2\times(2+5)=28\pi\)

　

当然，同じ結果になりました。

　

あとがき : 学校は教えない 「数学のよさ」

円柱の表面積 というのは中学校の教科書では必ず扱われる内容です。

(円錐の表面積 も同等)

で，円柱の表面積を決定する要素というのがありますよね？

そう，これさえ決まれば 表面積が決定する という変数・・・

円柱の表面積を決定する要素は，

底面の半径　と　高さ　です。

ということは，これらを「変数」とする方程式 (公式) が存在する。

それが　\(S=2\pi r(r+h)\)　です。

　

このように，簡単な公式ですが，学校の先生は伝えたがらない (私見) ・・・

もちろん，指導には目的・順序・個別最適化 という考えるべき要素がたくさんあり，

この件を否定するつもりはありません。

でも，こうやって式を一般化したり発展的に考えたりすることを「数学のよさ」と捉え，その機会を与えることもありなのでは？

などと　考えるわけで・・・