手順
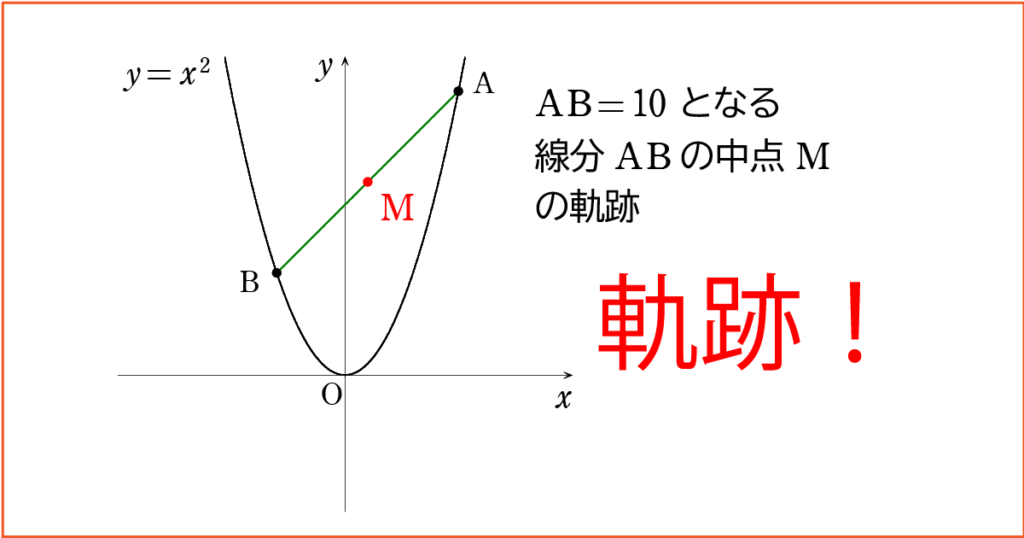
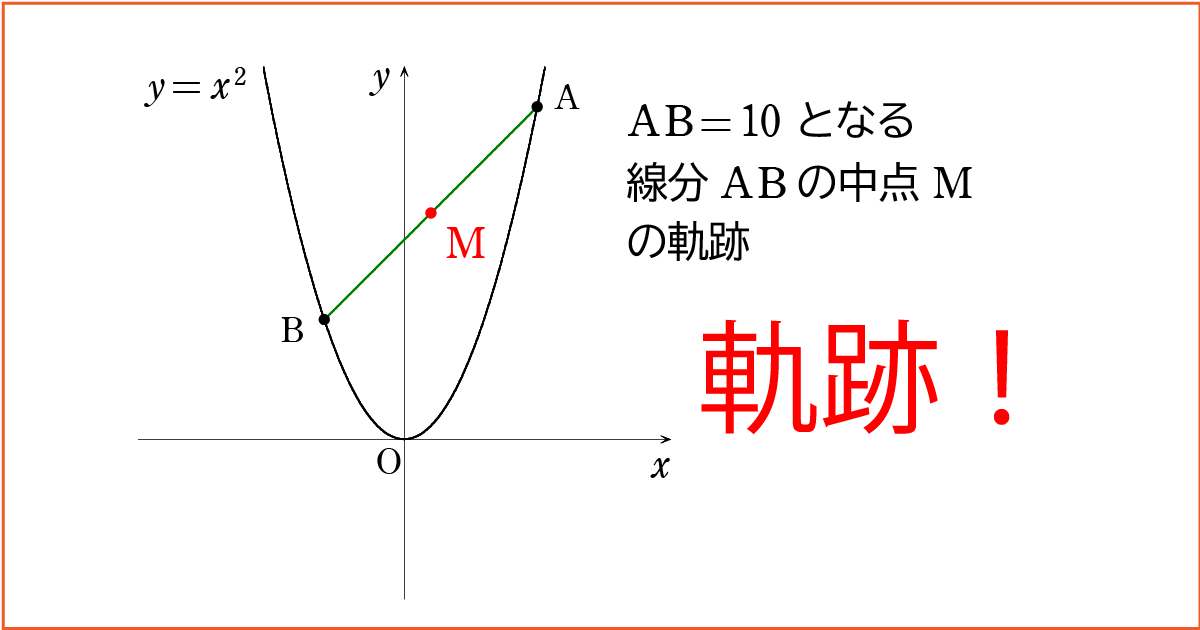
中点 M の軌跡を方程式で表すことを目指します。
中点 M の座標 を \(( x , y )\) ,
2 点 A, B の座標を A \((a,a^2)\) , B \(( b , b^2 )\) として
イロイロやってみましょう。
式をつくる
\(AB=10\) だから
\( AB^2=(b-a)^2+(b^2-a^2)^2=100 \) … ①
M \( (x , y ) \) は \((\frac{a+b}{2} , \frac{a^2+b^2}{2} )\) より
\(2x=a+b\) , \(2y=a^2+b^2 \) … ②
② より
\((a+b)^2=a^2+b^2+2ab\)\(=2y+2ab=4x^2\)
\(ab=2x^2-y\) … ③
\((a^2+b^2)^2=a^4+b^4+2(ab)^2\)
\(=4y^2\)
\(a^4+b^4=4y^2-2(ab)^2\) … ④
① の左辺を展開して
\(a^4+b^4+a^2+b^2-2a^2b^2-2ab=100\) \((4y^2-2a^2b^2)+2y-2a^2b^2-2ab=100\) \(4y^2-4(ab)^2+2y-2ab=100\)③ , ④ を代入して
\(4y^2-4(2x^2-y)^2+2y-2ab=100\) \(4y^2-4(4x^4-4x^2y+y^2)+2y-2(2x^2-y)=100\) \(-16x^4+16x^2y+4y-4x^2=100\)\(y\) について整理して
\((16x^2+4)y-16x^4-4x^2-100=0\)\(y=\frac{16x^4+4x^2+100)}{16x^2+4}\)
\(=\frac{x^2(16x^2+4)-4x^2+100}{16x^2+4}\)
\(=x^2-\frac{4x^2-100}{16x^2+4}\)
\(=x^2-\frac{\frac{1}{4}(16x^2+4)-101}{16x^2+4}\)
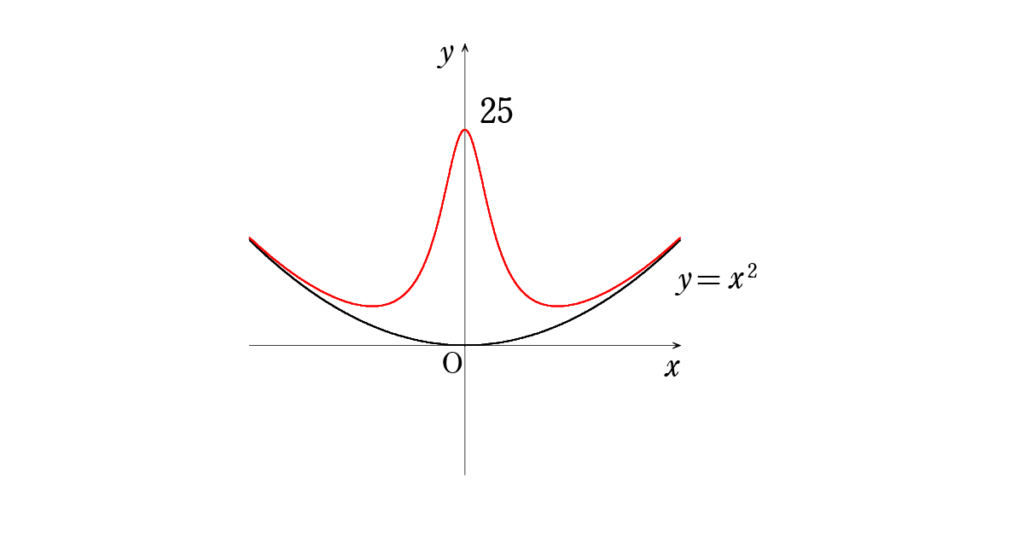
\(=x^2-\frac{1}{4}+\frac{101}{16x^2+4}\)





コメント