\(2025\) 項ならかき出すことも可能 (?) ですが,エレガントに解決したいものです。
いずれにしても,この数列の規則を知る必要があります。
数列の規則
数列を観察すると,
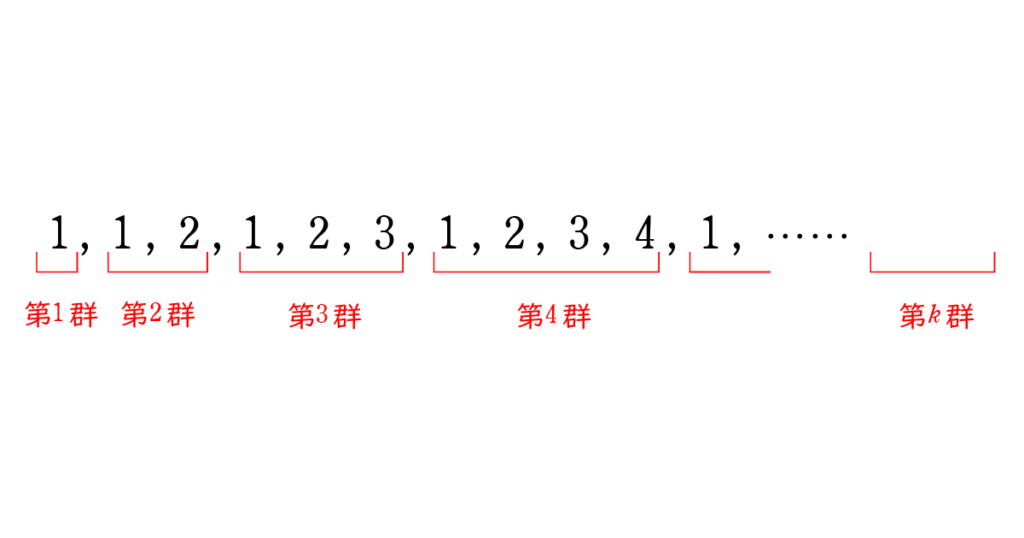
\(1\) \(1 , 2 \) \(1 , 2 , 3 \) \(1 , 2 , 3 , 4 \)と自然数の等差数列群がその項数を増やしながら並んでいることがわかります。
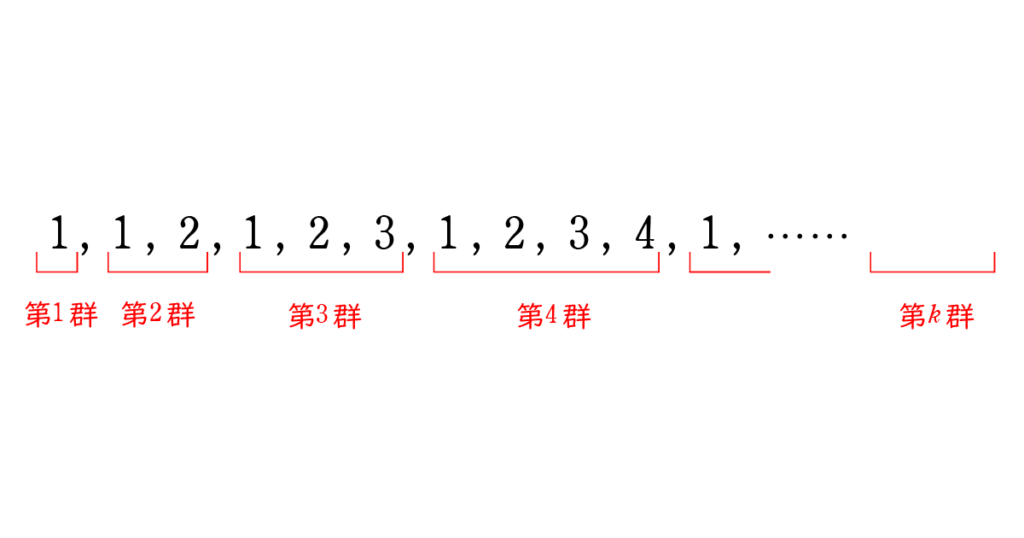
この等差数列群を,左から第 \(1\) 群,第 \(2\) 群,……
とすると図のようにかくことができます。
数列群による数列 [群数列]
数列群を 1 つの項とみると,新たな数列が生まれます。

その数列は,左から
\(1 , 2 , 3 , 4 , …… , k\)となり,数は それぞれの群における項数を表しています。
この数列 \(a_k\) は,
初項 \(1\) ,公差 \(1\) の等差数列だから
その一般項は \(a_k=k\) ですね!
第 \(2025\) 項は第何群?
数列をみると,例えば
第 \(3\) 項は 第 \(2\) 群
第 \(6\) 項は 第 \(3\) 群
第 \(10\) 項は 第 \(4\) 群 …
ということがわかります。
ところで,例に挙げた3項はそれぞれの群の最後の項です。
各群の最後の項が第何項であるか
第 \(1\) 群の最後の項は 第 \(1\) 項
第 \(2\) 群の最後の項は \(1+2\) から 第 \(3\) 項
第 \(3\) 群の最後の項は \(1+2+3\) から 第 \(6\) 項
と,「第 \(k\) 群の最後の項は 第 〇 項 です」という一般化ができそうですね。
\(\sum_{i=1}^{k} a_i =\sum_{i=1}^{k} i =\frac{1}{2}k(k+1) \)
第 \(k\) 群の最後の項は 第 \(\frac{1}{2}k(k+1) \) 項
第 \(2025\) 項が 第 \(k\) にあるとすると
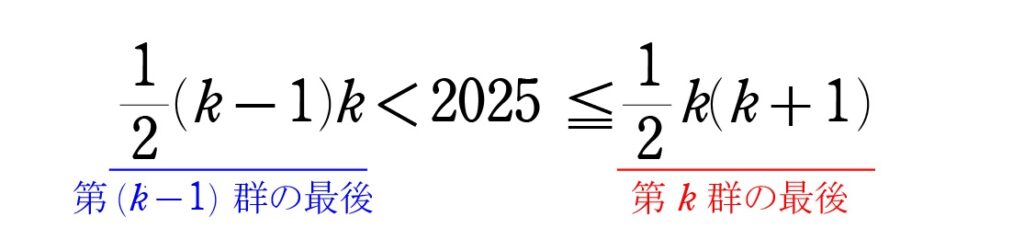
\(63\times64 = 4032 , 64\times65 = 4160 \) より
\(k=64\)
第 \(63\) 群の最後は
\(\frac{63\times64}{2}=2016\) より 第 \(2016\) 項
第 \(2025\) 項は 第 \(64\) 群の \((2025-2016=9)\) 番目だから \(9\)
あとがき : 数列は苦手とする人が多い!
どういうわけか,数列は「苦手」「難しい」と扱われる傾向にあります。
共通テスト 数学ⅡBC では (全4題から3第 を選ぶ) 選択問題として
④ 数列
⑤ 確率統計
⑥ ベクトル
⑦ 複素数平面
が与えられています。(2026 年)
私の選択(好み)は 数列 確率統計 複素数 で,
数列はむしろ 即解決しやすい部類なのです。
私の考えに反して避けられがちな数列ですが,そうなるのには理由があります。
苦手だと言い張る人ほど 式を大切にしないのです。
正確な式として表すことができなければ 直観勝負 に半分身を預ける状態になります。
直観勝負では泥沼にハマる一方で,成功することは無いでしょう。
直観勝負 を避けるためには,やはり式を正確に表すこと。
これは 「式は必ずかけ!」という意味ではありません。
どちらにしても 正確な式を明らかにすべきなのです。
群数列のように 複雑な変数事情をもつ課題なら,なおさらでしょう。
\(n\) や \(m\) をうまく扱い,全体を整理して立ち向かう習慣を!






コメント