弧度法による “弧の長さ”

弧の長さは

\((弧の長さ)=2\times(半径)\times\frac{(中心角)}{ 360^\circ}\)

と求めることは中学校までに学習しています。

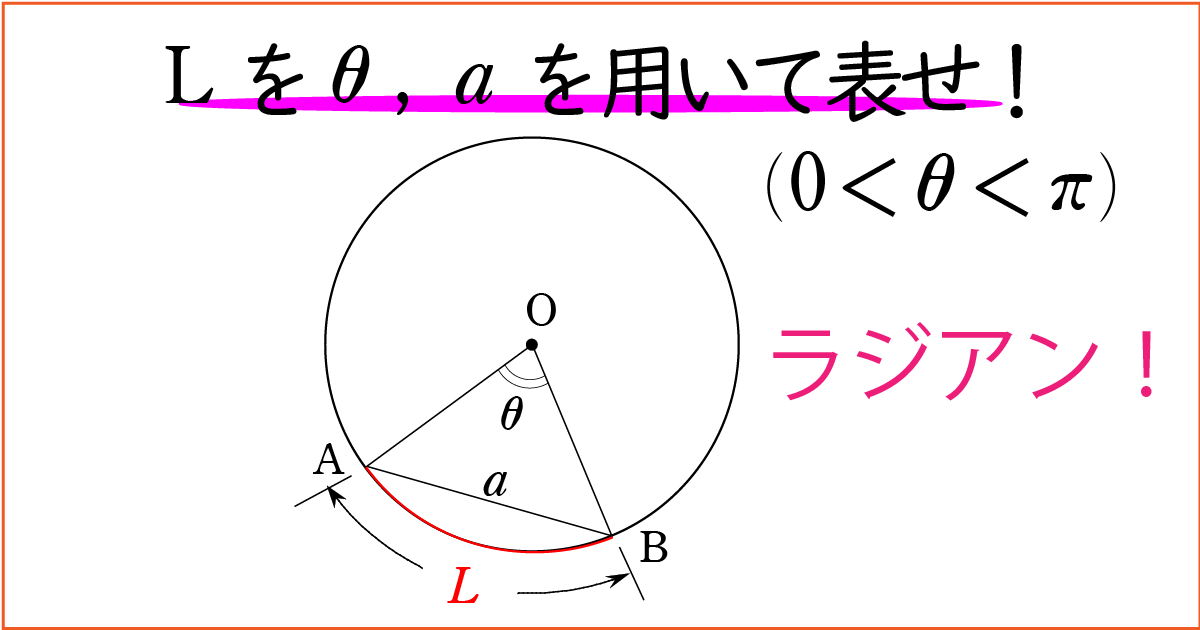
ここでは，弧度法で表された中心角　と　弦の長さ　

から “弧の長さ” を求める方法を考えます。

半径 \(r\) を定める

半径 \(r , 中心角 \theta ラジアンの弧の長さ L は \)

\(L=\theta r\)

と表されます。

本題では \(r\) は与えられていないので　これを定めることにしましょう。

△OAB に余弦定理を用いて

\(a^2=r^2+r^2-2 \times r \times r \times \cos{\theta} \) 　

　　\(　=2r^2 (1-\cos{\theta}) \)

よって　\(r=\frac{a}{\sqrt{2(1-\cos{\theta})}}\)　… ①

先に述べた通り，\(L=\theta r\) … ② が成り立ちます。

② に ① を代入し

\(L=\theta r \)

　\(=\frac{\theta}{\sqrt{2(1-\cos{\theta})}}a \)

本題のような課題を提示すると見えてくることがあります。

そう，弧度法の本質を理解していないという問題です。

まぁ，度数法と弧度法で表される角の大きさを互いに変換することは難しいことではないし，ほとんどの高校生は慣れによってスラスラとやってしまいます。

そして十分に慣れた頃に “本質” を問うと，理解の穴が露見されるわけです。

半径 \(1\) ，弧の長さ \(1\) のおうぎ形の中心角の大きさを \(1\) ラジアンとする。

これが定義で，度数法とは異なる用途をもつことが察せられます。