中学生なら 三平方の定理を,高校生なら 三角比の応用 を用いるのが一般的でしょうか。
ここでは,三平方の定理を利用した解法 と
三角比の応用 から導かれる公式
を紹介します。
解法 1 三平方の定理を利用

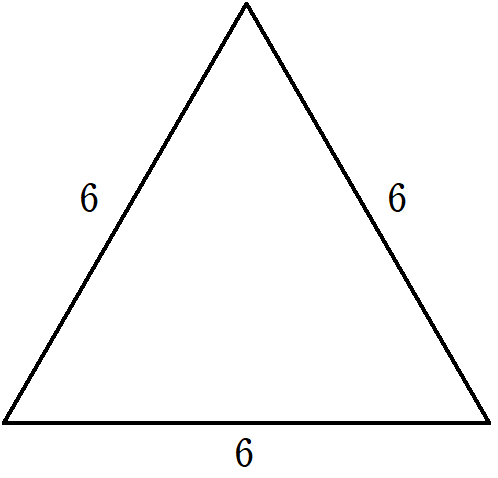
正三角形から,図のように直角三角形を見出すことができます。
内角が \(60^\circ\),\(30^\circ\) の特殊な直角三角形だから,
\(1 : 2 : \sqrt3\) の比を利用して
\(1 : 2 : \sqrt3 = 3 : 6 : (高さ h)\) , \(h=3\sqrt3\) となり
面積 \(S=\frac{1}{2}\times6\times3\sqrt3=9\sqrt3\)
となります。
解法 2 公式!
解法 1 や 高校数学で学習する 三角比の応用 から 正三角形の面積 の公式を導出できます。
公式を使うと
(面積) \( S=\frac{\sqrt3}{4}\times6^2=9\sqrt3\)
この公式を一般化すると
\(1\) 辺が \(a\) の正三角形の面積 \(S\) は
\(S=\frac{\sqrt3}{4}a^2\)となります。
時短テクニックとしてご活用ください!





コメント