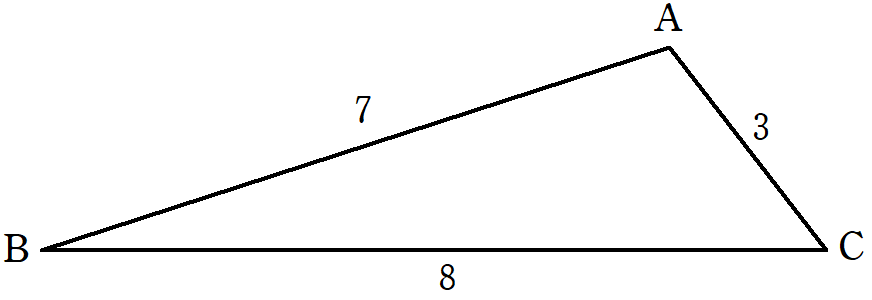
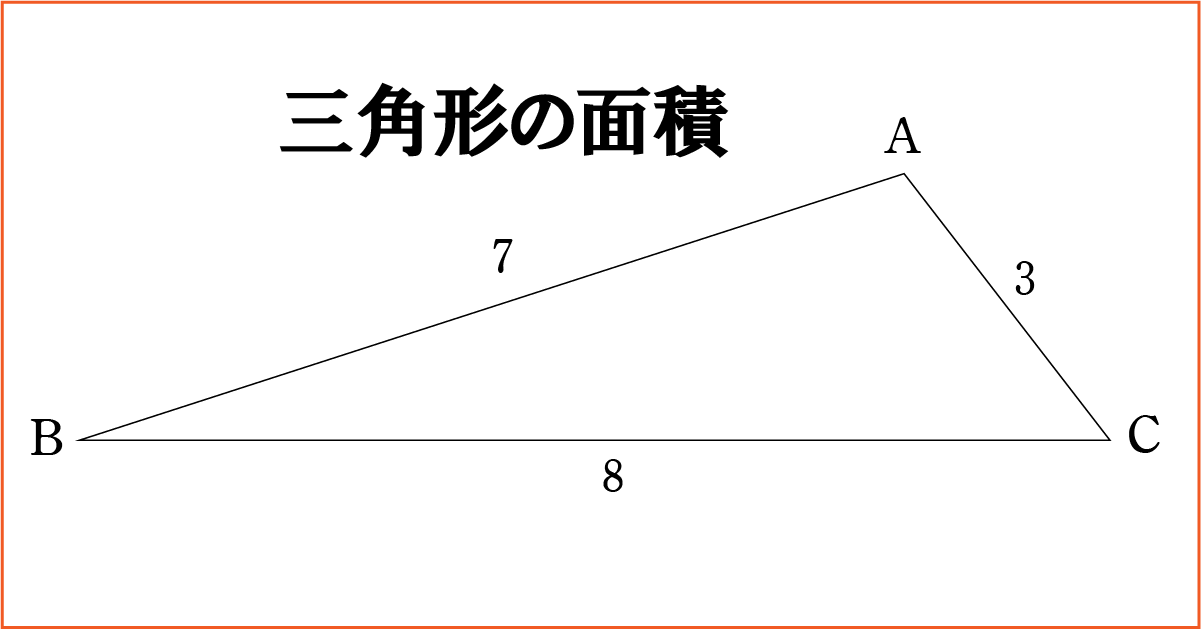
中学校の教科書にも登場する課題。
ここでは，中学校式の解法 と ヘロンの公式 を紹介します。
ヘロンの公式は 高校数学 で扱いますが，中学生でも十分に使いこなせます。
解法 1 中学校式 (高さを求める)
図のように，高さ \(h\)，や \(x\) を定めます。
△ABD に三平方の定理を利用して
\(x^2+h^2=7^2\)整理して \(x^2+h^2=49\) … ①
同様に △ACD にも
\(h^2+(8-x)^2=3^2\)整理して \(h^2+x^2-16x=-55\) … ②
① \(–\) ② により
\(16x=49+55\) \(x=\frac{13}{2}\)これを ① に代入して
\((\frac{13}{2})^2+h^2=49\) ，\(h^2=\frac{27}{4}\)
\(h>0\) だから \(h=\frac{3\sqrt3}{2}\)
面積 \(S=\frac{1}{2}\times8\times\frac{3\sqrt3}{2}=6\sqrt3\)
解法 2 ヘロンの公式 (数学 A)
こちらは高校の教科書に登場しますが，授業では扱われないことが多々あります(不思議)。
まず公式の確認から！
△ABC の \(3\) 辺 をそれぞれ \(a\) , \(b\) , \(c\) として
\(s=\frac{a+b+c}{2}\) (3 辺を足して 2 で割る)
これを用いて
面積 \(S=\sqrt{s(s-a)(s-b)(s-c)}\)
これを本題に利用すると
\(a=8\) , \(b=3\) , \(c=7\) だから
\(s=\frac{8+3+7}{2}=9\)面積 \(S=\sqrt{9(9-8)(9-3)(9-7)}=6\sqrt3\)
コメント