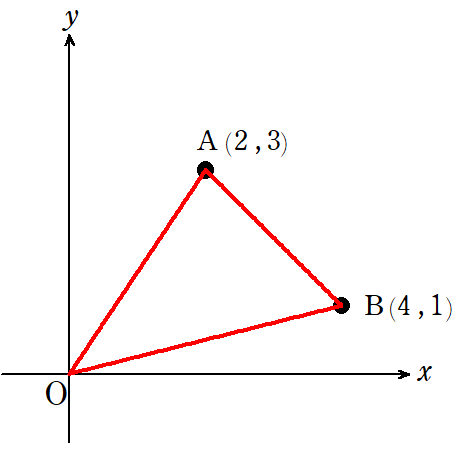
中学入試から大学入試まで頻出かつ応用力のある座標平面上の三角形の面積。
３ つの解法を紹介します。
解法 1 \((長方形)-(3 つの直角三角形)\)
図から，
縦 \(3\)，横 \(4\) の長方形 と，
底辺が \(2\)，高さが \(3\) の三角形，
底辺が \(2\)，高さが \(2\) の三角形，
底辺が \(4\)，高さが \(1\) の三角形
を見出すことができます。
青の直角三角形の面積 から ３ つの三角形の面積 を引いたものが求めたい三角形の面積である，とわかります。
ということで，
\(3\times4-\frac{1}{2}(2\times4+2\times2+4\times1)=5\)面積は \(5\) だとわかりました。
解法 2 等積変形
三角形の面積 \(S\) は \(S=\frac{1}{2}\times(底辺)\times(高さ)\) で求められます。
この底辺と高さを明らかにするために使うテクニックが 等積変形 です。
図のように，点 \(A\) を通り \(OB\) に平行な直線 \(ℓ\) を引きます。
線分 \(OB\) を底辺と決め，直線 \(ℓ\) 上に頂点をとると・・・
どこに頂点をとっても面積は一定 (変わらない) となるのです。
\(y\) 軸上に頂点 \(D\) をとると，この三角形が 線分 \(OD\) を底辺とする 高さ \(4\) の三角形だといえます。
〇 直線 \(ℓ\) の式を求める
直線 \(ℓ\) は \(OB\) に平行だから，その傾きは \(\frac{1}{4}\) となります。
直線 \(ℓ\) の式は \(y=\frac{1}{4}x+b\) ,
これに \(x=4 , y=1\) を代入して \(b=\frac{5}{2}\)
これが点 \(D\) の \(y\) 座標であり三角形の底辺の長さであるわけです。
〇 面積を求める
面積 \(S=\frac{1}{2}\times\frac{5}{2}\times4=5\)
解法 3 面積の公式 (10 秒で解けるよ！)
最後に紹介するのが，「平面ベクトル」で学習する「三角形の面積の公式」。
現在高校数学で扱っている内容ですが，公式は小中学生でも十分に使いこなせるものです。
面積 \(S=\frac{1}{2}|2\times1-4\times3|=5\)
とてもシンプルな式で求められましたね。
ここにある \(|2\times1-4\times3|\) は \((2\times1-4\times3=-10)\) の絶対値を表します。
まとめるとこうなります。
三角形 \(OAB\) の面積 \(S=\frac{1}{2}\times|(A の x 座標)\times(B の y 座標)-(B の x 座標)\times(A の y 座標)|\)
コメント